Next: GA Up: Optimization Algorithms Previous: ADPSO Contents
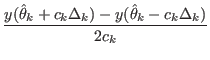 |
With
![]() the solution estimation at iteration
the solution estimation at iteration ![]() ,
, ![]() a learning
rate,
a learning
rate,
![]() the estimation of the gradient at
the estimation of the gradient at
![]() ,
, ![]() the objective function,
the objective function, ![]() a perturbation rate and
a perturbation rate and
![]() the randomized perturbation vector.
the randomized perturbation vector.
The current implementation performs this two-sided perturbation to estimate the
gradient with the perturbation vector ![]() drawn from a Bernoulli
drawn from a Bernoulli ![]() distribution to satisfy convergence conditions.
distribution to satisfy convergence conditions.
Table 3.6 lists the settings available for this optimizer.
| Name | Description |
|---|---|
| learning-rate | The learning rate |
| perturbation-rate | The rate |
| epsilon | The normalized maximum parameter step size. You
can use a mathematical expression for this
setting and use the variable |
| boundary-condition | Indicates how parameter boundaries should be handled. There are three possible settings: None (does not contrain the parameter space), StickResult (only constrains the actual solution to be within the parameter boundaries) and StickAll (constrains both the actual position and the perturbed solutions to be within the parameter boundaries). |
Jesse van den Kieboom 2014-02-26