Biorobotics Laboratory BioRob

Print

Fritz Menzer (Diploma Thesis 2004)

Modeling transient behaviour in vocal fold vibration using bifurcating nonlinear ordinary differential equation systems

Goals:

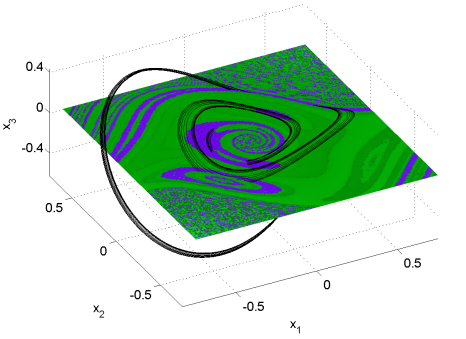This project deals with a wide range of topics. Stationary and transient vocal fold movement was analysed. In particular pitch breaks (sudden changes in the fundamental frequency) with a non-integer frequency ratio were found to be interesting because this case is different from the classic period-doubling scenario.

Modeling these pitch breaks with a system constructed like the Rössler system raised new hypotheses on pitch breaks. It turned out that some of these pitch breaks are not directly due to a bifurcation. Instead the system is perturbed to go from one attractor to another, both of which coexist for a given parameter range.

The model also raised the question if there may be a single mechanism responsible for pitch breaks to frequencies that are higher or lower than the normal vibration frequency.

A new physical model for the vocal folds was also developed, with the aim of keeping the number of state variables as low as possible. The result is a third order system having the contact area and the glottal airflow as state variables. In terms of the number of state variables this system is in the same class as a one-mass model driven by the glottal flow. However, it has more features than are usually found in a one-mass model. It also simulates the zipper-like opening and closing of the folds and takes into account a deformation of the vocal fold tissue.

An application of bifurcating nonlinear models could be to use them to drive real-time voice synthesis. This may contribute to a more natural sound. However, it must be considered that much of the naturalness of a sound has little to do with the vibration model itself, but with the way it is controlled.

Sounds - pitch break model

Sounds - Physical model driving a vocal tract model

Here is an example where the glottal flow of the physical model drives a vocal tract model (developed by Jack Mullen at the University of York). Normally this vocal tract model is driven by a waveform derived from the equations for glottal flow by Liljencrants and Fant (a.k.a. LF model).

It seems as if the voice source coming from the physical model produces less "buzziness" than the Lx waveform. Buzziness is an unwanted artifact of voice synthesizers. The LF model has this problem, probably because its derivative is discontinuous. On the other hand, the sound based on the simulated glottal flow sounds rather dull.

Odd stuff