Biorobotics Laboratory BioRob
BoxyBotII - Project Goals
Author: Benjamin Fankhauser, Assistants: A.Crespi, M.Perez, Contact: benjamin.fankhauser@epfl.ch
%20-%20small.jpg) |
This project aimed at designing a new version of the BoxyBot fish robot developped at the BIRG. It included among others:
|
-
BoxyBot II - Final Report.pdf
BoxyBot II - Final Presentation.pdf
BoxyBot II - Final Presentation.pps
BoxyBotII - Programmation and Control
|
The Command of the BoxyBot was done using a Central Pattern Generator (CPG). This meant implementing a system of four coupled amplitude-controlled phase oscillators. The CPG allowed us to change amplitude, frequency and offset of every articulation online and would at the same time guarantee a smooth change. |
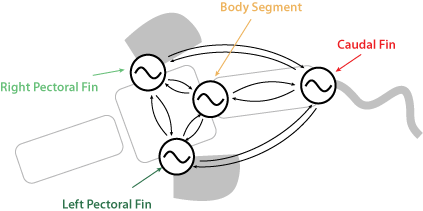 |
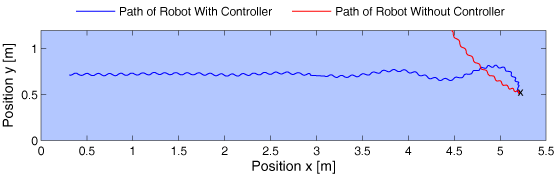 |
The position of the robot could be aquired by two cameras placed above the pool. The control was done by means of a proportional controller in order to make the robot follow a straight line. |
BoxBotII - Fin Design and Testing
|
Influence of Resonance Frequency To design fins that efficiently made the robot swim fast, we wanted to show the influence of the resonance frequency fR on the speed of the robot. As the graph shows, the fin's resonance frequency (i.e. maximal amlitdue) is at 0.7 Hz. At the same time we can observe that the speed increases less for higher frequencies. Efficiency Estimation Efficiency estimation measures using the Strouhal number proofed that swimming at the resonance frequency of the fin is very efficient. |
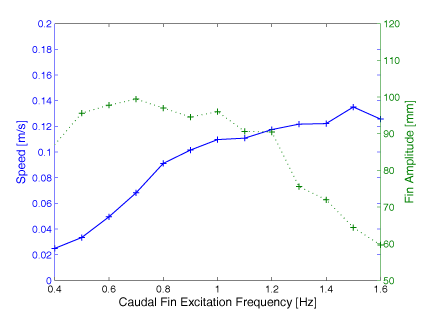 |
|
Influence of Excitation Amplitude and Heigth of Fin We could show that higher excitation amplitude resulted in higher speed. Caudal and Pectoral Fins It could be shown that the movement of caudal and pectoral fins is interfering and movement of the two types of fins at the same time results in slower speed, than using only the caudal fin (cf. video). |
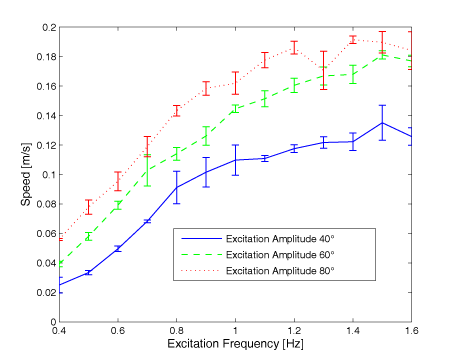
|
-
BoxyBotII - CaudalFin BodySegment (3 MB).avi
BoxyBotII - Pectoral Fins (2 MB).avi
BoxyBotII - All Fins (3 MB).avi
BoxyBotII - Simulation
|
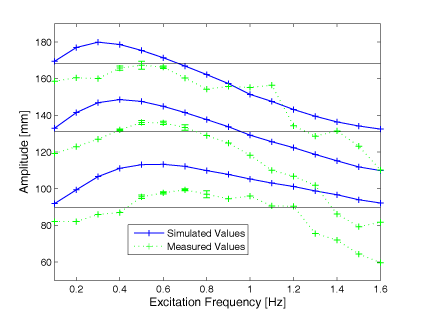
Fin Amplitude It could be shown that the results for the amplitude of the fin were comparable to reality. The graph shows the measured and simulated amplitude of a caudal fin of 95 x 60 mm, for respectively 40°, 60° and 80° excitation amplitude. The black lines show the amplitude of rigid fin of same size. |
|
- Archived student projects
- Alain Dysli
- Alexandre Tuleu
- Anurag Tripathi
- Ariane Pasquier
- Aïsha Hitz
- Barthélémy von Haller
- Benjamin Fankhauser
- Benoit Rat
- Bertrand Mesot
- Biljana Petreska
- Brian Jimenez
- Christian Lathion
- Christophe Richon
- Cédric Favre
- Daisy Lachat
- Daniel Marbach
- Daniel Marbach
- Elia Palme
- Elmar Dittrich
- Etienne Dysli
- Fabrizio Patuzzo
- Fritz Menzer
- Giorgio Brambilla
- Ivan Kviatkevitch
- Jean-Christophe Fillion-Robin
- Jean-Philippe Egger
- Jennifer Meinen
- Jesse van den Kieboom
- Jocelyne Lotfi
- Julia Jesse
- Julien Gagnet
- Julien Nicolas
- Julien Ruffin
- Jérôme Braure
- Jérôme Guerra
- Jérôme Maye
- Jérôme Maye
- Kevin Drapel & Cyril Jaquier
- Kevin Drapel & Cyril Jaquier
- Loïc Matthey
- Ludovic Righetti
- Lukas Benda
- Lukas Hohl
- Lukas Hohl
- Marc-Antoine Nüssli
- Martin Biehl
- Martin Riess
- Martin Rumo
- Mathieu Salzmann
- Matteo Thomas de Giacomi
- Matteo Thomas de Giacomi
- Michael Gerber
- Michel Ganguin
- Michel Yerly
- Mikaël Mayer
- Muhamed Mehmedinovic
- Neha Priyadarshini Garg
- Nicolas Delieutraz
- Panteleimon Zotos
- Pascal Cominoli
- Pascal Cominoli
- Patrick Amstutz
- Pedro Lopez Estepa
- Pierre-Arnaud Guyot
- Rafael Arco Arredondo
- Raphaël Haberer-Proust
- Rico Möckel
- Sacha Contantinescu
- Sandra Wieser
- Sarah Marthe
- Simon Blanchoud
- Simon Capern
- Simon Lépine
- Simon Ruffieux
- Simon Rutishauser
- Stephan Singh
- Stéphane Mojon
- Stéphane Mojon
- Sébastian Gay
- Vlad Trifa
- Yvan Bourquin
