Biorobotics Laboratory BioRob

Locomotion Exploiting Body Dynamics

In vertebrates, the Central Pattern Generator (CPG) is a network of neurons located in the spinal cord capable of producing oscillatory output used as basic rythm for body movement.

Non-linear oscillators are systems of differential equations having many desirable properties such as robustness, independence from initial conditions and synchronisation. For this reason, legged robotics has much to gain by implementing a CPG using those systems.

The objective of this project is the realisation robust and controllable CPG based Hopf Oscillators able to generate a gallopping gait in a real four legged robot endowed with passive dynamics. Different techniques to obtain a turning movement in such a robot are also explored.

The Puppy II Robot

Puppy II is a quadruped robot with passive dynamics. Movement of the legs is obtained by four hip motors, while the passive dynamics is provided by springs on each knee joint.

Feedback from the environment is obtained by four force sensitive sensors on the feets, four potentiometers on the passive joints to measure joint angles, one inertial sensor, one infrared sensor in the front and three touch sensors on its back, trunk and body.

Not having any battery and embedded processor, the robot has a very low degree of energetic and computational autonomy, so that it has to be permamently connected to a power source and to a computer providing the computation of the legs motor set points through USB.

Controllable parameters are amplitude, frequency and center of oscillation of each of the four legs.

Straight Locomotion

We measured the speed reachable by the robot by varying the amplitude of movement and frequency of oscillation of its legs and measuring the space covered over 5 seconds.

The graph shows in color the reached speed in meters per second. The achiavable speed appears to be proportional to those two parameters with amplitude smaller than 200 motor steps and frequency smaller than 3.58Hz. If one or both of those values are reached, the quality of movement of the robot rapidly degradates. Bigger amplitudes or frequencies, and so higher speeds, may probably be achieved on a surfaces with higher friction coefficient, but tests are needed to verify this hypothesis.

We can also observe that both amplitude and frequency can be useful to control the robot speed, however selecting a specific frequency and modifying the amplitude of movement seems to be a better way to obtain a precise control of the robot's speed in the range of allowed parameters previously described.
Moreover, we also believe that this type of control is "healthier" for the robot, as it seems to be less energy-consuming.

Turning Using Setpoint Control

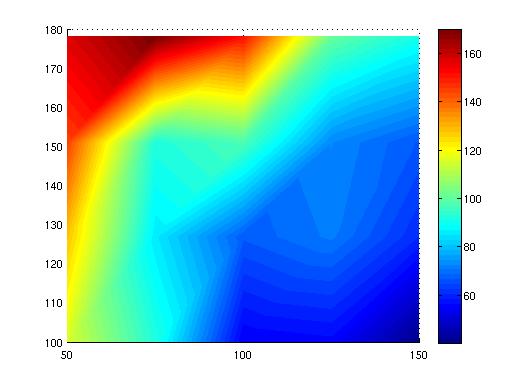
Setpoint control consists in modifying the centers of oscillations the robot's legs.

If the two left legs are approached ba a small value s and the distance between the two right legs is increased by the same small value s, the robot's body tilts to its right side and so, turn.

The graph shows in color the turning radius in centimeters. Amplitude is measured in motor steps, one motor step corresponding to approximatively 0.05 degrees.

It turned out that the robot's turning radius is proportional to the variation of distance s between the legs and inversely proportional to their amplitude of oscillation.

Turning Using Amplitude Control

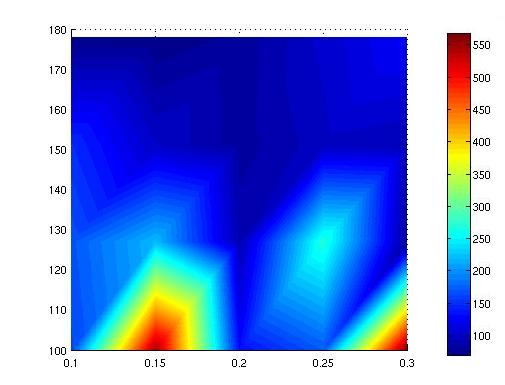
Amplitude control consists in control the amplitude of the two pairs of ipsilateral legs.

To obtain a left turn we will have to increase the amplitude of the right legs and decrease the amplitude of the left legs.

The graph represents in color the turning radius in centimeters. On vertical axis, amplitude in motor steps is represented (one motor step corresponds to approximatively 0.05 degrees), on horizontal axis percentage of increase/decrease of amplitude of oscillation on a pair of ipsilateral legs (i.e. 0.1 means that two legs oscillates at 110% of their original amplitude, while their opposite legs oscillates at 90% of the original value).

We observe that with amplitudes higher than 150 motor steps, the turning radius of the robot tends to stabilize around a constant value (between 100 and 150 cm) with all values of amplitude variation used in our set of tests.
At small amplitudes we observe the emergence of precisely localized peaks around specific values of amplitude variation, i.e. 0.15 and 0.3. In these conditions, the robot doesn't seem able to turn. In some test we even observed that the robot even tended to drift in the wrong direction.