Biorobotics Laboratory BioRob

Print

Abstract

Animals have demonstrated an impressive adaptive behavior along evolution, allowing them to survive into hostile and constantly changing environments. Such a level of adaptation is possible because the neuronal structure of the animal is not prenatally determined and it does not remain fixed throughout the entire life of the organism, but is shaped according to experience. A mechanism called synaptic plasticity performs such short and long-term modifications of the connections in the brain.

Our goal was to implement and perform a qualitative analysis of an interesting model of associative memory based on coupled oscillators, that is able to learn input signals by adapting the natural frequencies of the oscillators. In the second part of this project, we describe a new model of memory we have developed by modifying the oscillator we analyzed by adding some interesting features, and we show that this new model is able theoretically to learn any kind of periodic complex signal. Finally, we show that our model is extremely robust when the presented signal is noisy, or when the oscillators are unreliable and can fail.

Our work should not be considered as an attempt to find a universal model able to perform the same tasks as the animal brain with comparable performance, but rather as an attempt to show that it is possible, at least from a mathematical point of view, to learn any periodic complex signal using a network coupled oscillating systems that mutually influence their behavior according to the relationship between their respective phases.

Results

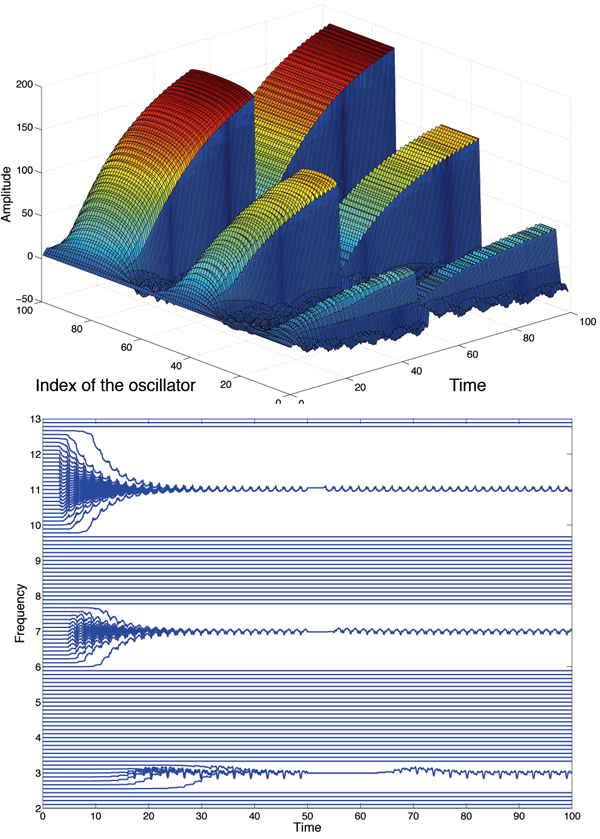Our starting point was to take inspiration from an novel model of oscillatory associative memory and analyze its properties and weaknesses. As a second goal, we needed to try to find some techniques in order to improve this model by trying to get it rid off its major drawbacks. As you can see on the image above, while a complex signal f(x)=sin(3x) + 2*sin(7x)+4*sin(11x) is presented to the network, some oscillators will change their frequency to neighboring frequency component. We can then know if a signal has been learned or not simply by looking the amount of oscillators having a synchronous activity, and deduce if the signal has been already presented to the network or not.

Download

Here you can download some files related to this project: