Biorobotics Laboratory BioRob

Print

ROBUSTNESS IN POPULATION OF COUPLED OSCILLATORS



Jérôme Guerra, Master Thesis, winter 2004-2005

Supervisors : Jonas Buchli and Auke Jan Ijspeert

abstract

This report is an exploration of the robustness of populations of coupled amplitude controlled phase oscillators (ACPO). This kind of system presents interesting properties for robustness against perturbations. To show this robustness, I propose a model of perturbations like exposition to heat, local breakdowns or aging. Then I present results, obtained with the numerical simulation of the behavior of, populations of oscillators under this model of perturbations, and I propose two applications: a robust sinus wave generator and a robust square wave generator. The results are discussed in terms of profit or loss of the system's robustness. This work has been done in the frame of the Master Thesis in Computer Sciences at Swiss Federal Institute of Technology.

Results

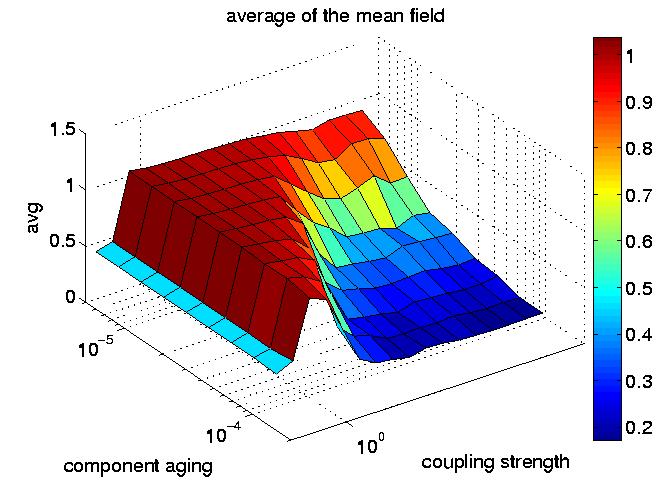
All results presented have produced by the numerical integration of the differential equation of a population of coupled ACPO. The coupling is variable from no coupling to globally coupled.
The essential part of this work consists in observation of the behavior of such system, population of oscillators, under the effects of perturbations.
The perturbations implemented are :
-Thermal noise
-Component aging
-Fabrication fault
-Breakdowns

Sinus wave generator


The first application made with a population of coupled oscillators is a sinus wave generator.

Previous figure shows the the lost of synchronization due to an increase of fabrication default.


Breadowns


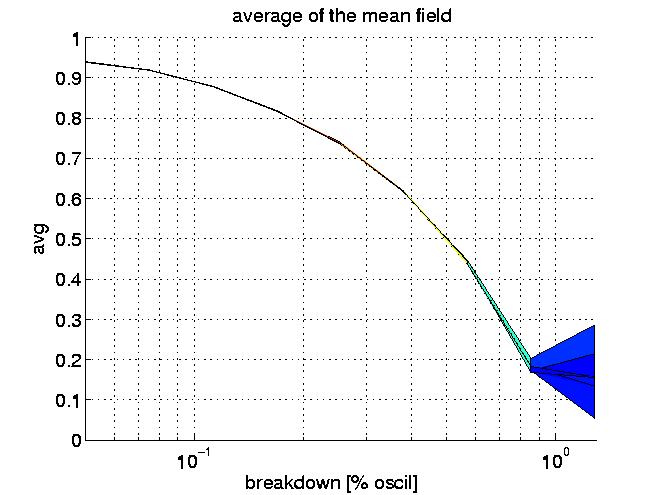
The sinus wave generator presents a astonishing robustness to breakdowns. For example in the case presented where breakdowns are on oscillators. As one can see the degradation of the system (synchronization) is linear but the frequency of the generator remains erfectly stable until more than 70% oscillators breaks.

Square wave generator


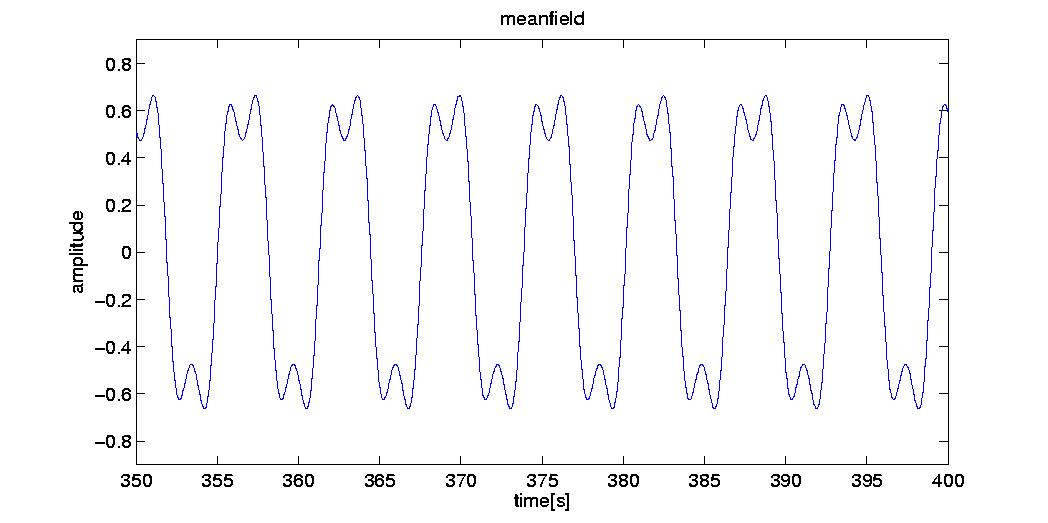
The square wave generator is built with a bi-clustered population of ACPO.
In order to approximate the Fourier series of a square wave, the second cluster contains oscillators with a three times higher intrinsic frequency than the second cluster, and is also composed by three times less oscillators.
Previous figure is the mean field resulting.

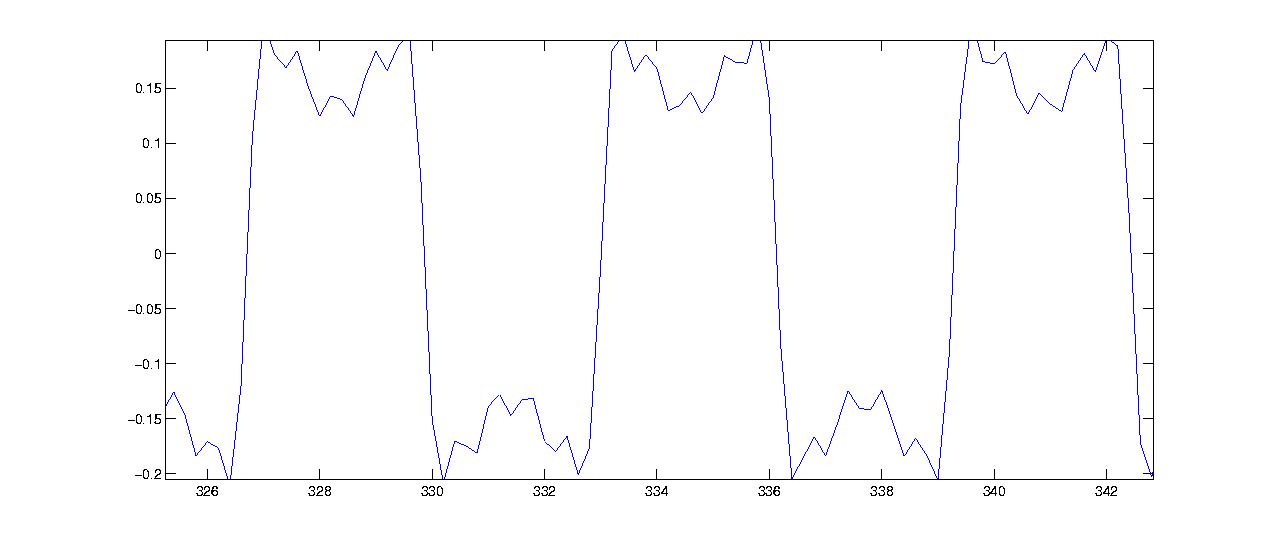With a population with five clusters the approximation is, as you can see in previous figure, better.