Biorobotics Laboratory BioRob

Print

Yvan Bourquin - Modular Walkers

Self-Organization of Locomotion in Modular Robots

Abstract

The Biologically Inspired Robotics Group (BIRG) of the Swiss Federal Institute of Technology in Lausanne (EPFL) is developing new hardware and software for an experimental modular robotic platform. Modular robots are robots built of several similar building blocks called modules. Usually modules have one or two hinges that allow movement with one or two degrees of freedom. Locomotion of the robot, e.g. crawling, is possible when several modules are put together.

By means of computer simulations, this study explores the self-organization of locomotion in various assemblage configuration of the BIRG's robot. Locomotion is enabled by the regular oscillations of the motors, which are produced by Central Pattern Generators (CPG) inspired from the nervous system of vertebrates. Optimal oscillatory parameters are found using different numerical search methods: genetic algorithms, simulated annealing, particle swarm optimisation and random search. Although all these methods generate efficient locomotion patterns, the best results are obtained by particle swarm optimization.

Modular Robots

The idea behind modular robotics is freely inspired by cellular automata and by social insects. Through cooperation, social insects, such as ants, bees or termites, achieve feats that would be impossible to achieve by a single individual. For example, ants can use their own body as bridge to allow other ants to move safely above a crag. By using similar principles, modular robots perform self-reconfiguration, e.g. they autonomously change their shape and adapt to different kinds of terrain. For example, some modular robots can transform into a snake to tunnel through a pipe then later transform into a quadruped to go up stairs or even climb a fence.


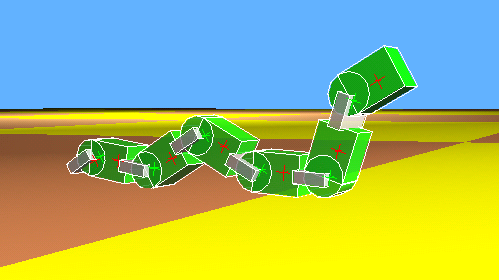
Figure 1: Caterpillar configuration.

Locomotion

Locomotion is an essential skill in animals. It is required for hunting preys, escaping predators, or more generally, finding food and mates. Locomotion is achieved by applying forces on a terrestrial, aerial or aquatic environment. These forces are generated by the rhythmic contraction of muscles attached to limbs; wings, legs, fins and so on.

This document is concerned only with locomotion on a flat ground surface and under gravitational force. A locomotory gait is efficient when all the involved muscles contract and extend with the same frequency. Typical terrestrial legged locomotion gaits are walk, trot and bound.

Oscillators

Generally, locomotion in modular robots is achieved using simple state automata; at every time step, state values, representing desired joint angles, are fetched from a gait table and applied to the corresponding servomotors. However, in this project, a quite different approach is used. Locomotion is simulated using non-linear oscillators as motor controllers as it was proposed in [Ijspeert, et al. 2003]. These oscillators are defined by two differential equations:


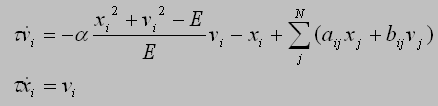
This type of oscillator converges to a smooth sine wave which amplitude and frequency can be controlled. The oscillations' phase shift depends on the coupling strength between the oscillators. The coupling strengths and the oscillations' angles and amplitudes are the free parameters that are explored with numerical optimization algorithms.

Numerical Optimization

Tuning controllers parameters for locomotion is a multi-dimensional optimization problem that consists in finding the optimum of a function of several independent variable such that Ф = f(p1, p2, p3 ... pN) and where Ф must be optimized. Some optimization problems can be solved analytically or by gradient descent methods. However, with many real world problems, these methods do not work because f(...) cannot be described by a simple formula. This is the case for the current problem where f(...) is computed by the complex algorithms of the physics simulator.

Some methods such as the downhill simplex can perform optimization without requiring gradient information. Unfortunately, such non-stochastic methods suffer from their inability to escape from local minima. Therefore, methods involving a random variable are preferred. Three such methods were chosen to optimize our controllers: genetic algorithms (GA), simulated annealing (SA) and particles swarm optimization (PSO).


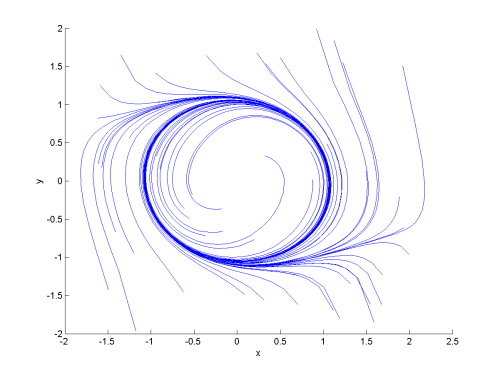
Figure 2: Oscillator's limit cycle.

Particle Swarm Optimization

Particle Swarm Optimisation (PSO) was developed in 1995 by James Kennedy and Russell Eberhart [Kennedy, et al. 1995]. Like genetic algorithms, PSO is based on a population that slowly converges towards one or more solutions. However, with PSO, the particles are preserved throughout the entire process; they do not die. Contrary to GA, which is based on competition for better chances of survival and reproduction, PSO uses a kind of cooperation between the particles. This is achieved through the exchange of the coordinates of the best solutions that have been encountered so far.


Figure 3: Quadruped configuration

Results

All three search methods were found efficient gaits. For example quadruped morphologies (Figure 3) developped gaits similar to animal quadrupeds. The caterpillar configuration (Figure 1) developed a kind of rolling motion similar to the caterpillar of a tracked vehicle and sometimes a kind of worm-like locomotion.


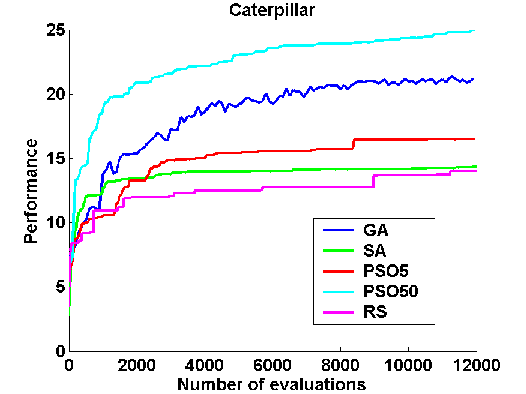
Figure 4: Results compared.

For all morphologies the most efficient search algorithm was always the particle swarm optimization (PSO50). See results for the caterpillar configuration in Figure 4.

Conclusion

Interestingly, the four search methods all produced similar and good results. The biggest surprise was that particle swarm optimization delivered constantly better results than the genetic algorithms. The myth that genetic algorithms is a superior optimization technique is a bit broken. In fact, genetic algorithms are not superior but their popularity in evolutionary robotics is mostly due to their nature, inspired from phylogeny, which fits very well with the concept of artificial life or artificial intelligence. This project has shown that PSO works just as well, or even better than GAs, to optimize controllers.

However, we should also avoid generalising the results from this experiment. GA, SA and PSO all use a number of control parameters, e.g. population size, swarm size, mutation rate and so on. These control parameters have a great influence on the results. In this project, the control parameters of the algorithms have been chosen intuitively by the author, but in fact, they would need to be optimized themselves.

Links

Sample Videos (DivX-5.0) and MPEG-1

References